Dicas para facilitar Cálculos simples

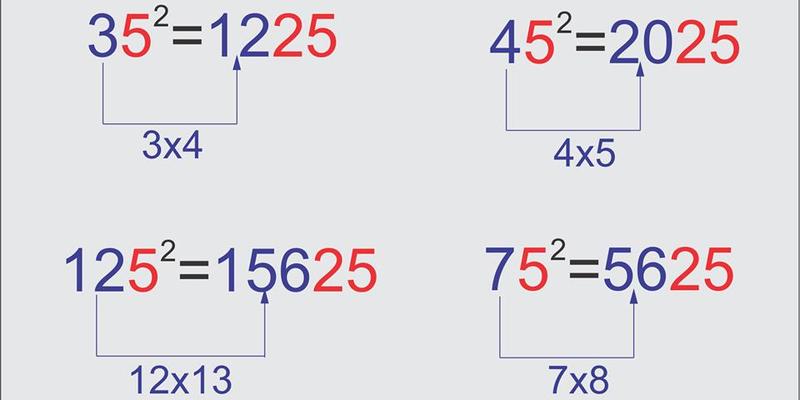
Dica 1: Multiplicação difícil

Se você possui uma multiplicação de números grandes você pode facilmente subdividir para chegar à resposta, observe:
32×125, é o mesmo que:
16×250 é o mesmo que:
8×500 é o mesmo que:
4×1000 = 4000

Dica 2: Multiplicar um número por 10

Basta deslocar a vírgula uma casa decimal para a direita.
Exemplo 1: 14×10 = 140
Exemplo 2: 16,530 x 10 = 165,30

Dica 3: Multiplique por 5

Basta multiplicar por 10 e dividir por 2.
Exemplo 1: 7×5 = 70/2 = 35
Exemplo 2: 9×5 = 90/2 = 45

Dica 4: Multiplique por 6

Basta multiplicar por 3 e então 2.
Exemplo 1: 7×6 = 21×2 = 42
Exemplo 2: 15×6 = 45×2 = 90

Dica 5: Multiplique por 9

Basta multiplicar por 10 e subtrair o número original.
Exemplo 1: 8×9 = 80 – 8 = 72
Exemplo 2: 13×9 = 130 – 13 = 117

Dica 6: Divida por 10

Basta deslocar a vírgula uma casa decimal para a esquerda.
Exemplo 1: 14 ÷ 10 = 1,4
Exemplo 2: 16,530 ÷ 10 = 1,6530

Dica 7: Multiplicando por 11 (número de 2 algarismos)

Some os algarismos do número e coloque o resultado no meio dele.
Exemplo 1:  23×11
somamos os algarismos do número 23: 2+3=5
colocamos o resultado no meio deles: 253. Portanto 23×11 = 253.
Exemplo 2:  63×11
somamos os algarismos do número 63: 6+3=9
colocamos o resultado no meio deles: 693. Portanto 63×11 = 693.
Exemplo 3:  91×11
somamos os algarismos do número 91: 9+1=10
Como deu um nº maior que 9, então não podemos colocar todo o número no meio deles. Colocamos apenas o algarismo das unidades (0) no meio deles, e o algarismo da dezena (1) é somado ao primeiro algarismo do número: 1001. Portanto 91×11 = 1001.

Dica 7.1: Multiplicando um número de 1 algarismo por 11

Basta multiplicar por 10, e somar o número inicial.
Exemplo 1: 7×11 = 70 + 7 = 77
Exemplo 2: 5×11 = 50 + 5 = 55
Exemplo 3: 9×11 = 90 + 9 = 99

Dica 8: Multiplique por 12

Basta multiplicar por 10 e somar com o dobro do número original.
Exemplo 1: 7×12
Multiplique 7×10 = 70, depois some com o dobro de 7 que é 2×7 = 14
Portanto, 7×12 = 70+14 = 84
Exemplo 2: 9×12 = 90 + 18 = 108
Exemplo 3: 6×12 = 60 + 12 = 72
Exemplo 4: 16×12 = 160 + 32 = 192

Dica 9: Multiplique por 15

Basta multiplicar por o número original por 10 e soma-lo a sua metade.
Exemplo 1: 9×15
Faça assim: 9×10 = 90, a metade de 90 é 45, então some 90+45.
Portanto 9×15 = 90+45 = 135
Exemplo 2: 5×15 = 50+25 = 75
Exemplo 3: 12×15 = 120+60 = 180
Exemplo 4: 27×15 = 270+135 = 405

Dica 10: Multiplique por 100

Basta acrescentar/andar 2 zeros e/ou duas casas a direita.
Exemplo 1: 7×100 = 700
Exemplo 2: 12×100 = 1200
Exemplo 3: 12,35×100 =1235
Exemplo 4: 29,1×100 = 2910

Dica 11: Multiplique por 99

Basta acrescentar 2 zeros no final do número e subtrair pelo número inicial.
Exemplo 1: 34×99
Acrescentamos dois zeros no final do número 34, assim 3400
Agora subtraímos o número inicial, 3400 – 34 = 3366
Portanto: 34×99 =  3400 – 34 = 3366
Exemplo 2: 15×99 = 1500 – 15 = 1485
Exemplo 3: 50×99 = 5000 – 50 = 4950
Exemplo 4: 2,5×99 = 250 – 2,5 = 247,5

Dica 12: Soma dos n primeiros números naturais ímpares:

A soma dos n primeiros números naturais ímpares é igual a n². Exemplos:
Exemplo 1: Soma dos 5 primeiros números naturais ímpares (1+3+5+7+9), é igual a 5² = 25.
Exemplo 2: 1+3+5+7+9+11 = 6²
Exemplo 2: 1+3+5+7+9+11+13 = 7²

Bons estudos, atenciosamente Professor Leonardo Bezerra.

Resoluções comentadas - Exame de seleção do IFRN 2015 e 2016.

Resolução 2016

 Resolução 2015

OBS: Vídeos Cedidos pelo Prof. Marcos.

Bons estudos!

Aprenda tabuada de forma fácil em horas, não em semanas! [e-book]

Se você é professor de Matemática do Ensino Fundamental 1 ou 2, ou porque não do Ensino Médio, com certeza já passou pela situação de durante uma aula, perguntar quanto é 8 vezes 7 e escutar o silêncio do aluno.

Se você é um estudante que se enquadra em um destes níveis de ensino citados acima, tenho a certeza que se sente desanimado em continuar a estudar Matemática porque simplesmente não conseguiu aprender a tabuada. Não entrarei no mérito do professor em conseguir ou não fazer os seus alunos aprenderem a tabuada.

Discutir onde estão os erros, seja em aluno ou professor nunca é a melhor alternativa. A melhor saída é buscar formas diferentes e/ou complementares de se ensinar qualquer conteúdo matemático de forma eficaz.

Tente avaliar quando a sua didática e metodologia não funcionam para todos os seus alunos, e aí sim é hora de procurar outros meios. Qualquer ajuda é bem-vinda e deve ser testada em busca do melhor aprendizado dos nossos alunos.

O título do post parece pretensioso do ponto de vista de quem ensina, mas do ponto de vista de quem aprende é sempre uma barreira. Conheça o e-book Tabuada Fácil - Método de Aprendizado, e aprenda a tabuada usando esse método.

O que é a Tabuada Fácil?

A Tabuada Fácil é um e-book que busca ensinar de forma prática e eficaz a tabuada. No método convencional a criança precisa decorar uma quantidade grande de números que não tem muito sentido para ela.

Até nós adultos temos dificuldades em lembrar alguns resultados da tabuada. Mas com o método da tabuada Fácil a criança aprende de forma objetiva e prática, gerando o entendimento não pela decoração mas sim pela assimilação do conteúdo. Assim ela se lembrará dos resultados com muita facilidade e naturalidade.

Tive acesso ao material e como professor de Matemática, aprovo o método. Toda a alternativa que colabora para o melhoramento da aprendizagem do aluno é bem-vinda e merece ser conhecido por pais e alunos.

Acesse, conheça, se puder compre e divulgue esse e-book para crianças, adolescentes e adultos que querem aprender a tabuada.

 

Fonte: Blog do Prof. Edigley Alexandre

Produtos Notáveis

Considerações iniciais

Os conceitos sobre os produtos notáveis merecem muita atenção, pois seu uso facilita cálculos, reduz o tempo de resolução e agiliza o aprendizado. O conhecimento dessa ferramenta não implica dizer que não necessitamos saber o desenvolvimento do cálculo proposto, apenas que temos mais caminhos convergentes à solução final.  Utilizamos o termo notável para apontar sua importância, sua notabilidade e sua carência de atenção.

Os gregos, na antiguidade, faziam uso de procedimentos algébricos e geométricos exatamente iguais aos produtos notáveis modernos. É importante destacar que o uso de sua maioria foi atribuído aos pitagóricos e estão registrados na obra de Euclides de Alexandria Elementos na forma de representações geométricas.

Ao lidarmos com operações algébricas, perceberemos que alguns polinômios aparecem frequentemente e, ainda, exibem certa regularidade. Esses são os produtos notáveis. Aqui estudaremos o quadrado da soma de dois termos, o quadrado da diferença de dois termos, o produto da soma pela diferença de dois temos, o cubo da soma de dois termos e, por fim, o cubo da diferença de dois termos. Vamos à explanação de cada um deles.

1.    O quadrado da soma de dois termos

Verifiquem a representação e utilização da propriedade da potenciação em seu desenvolvimento.

(a + b)² = (a + b) . (a + b)

Onde a é o primeiro termo e b é o segundo.

Ao desenvolvermos esse produto, utilizando a propriedade distributiva da multiplicação, teremos:

O quadrado da soma de dois termos é igual ao quadrado do primeiro termo, mais duas vezes o produto do primeiro termo pelo segundo, mais o quadrado do segundo termo.

Exemplos

2.    O quadrado da diferença de dois termos

Seguindo o critério do item anterior, temos:

(a - b)² = (a - b) . (a - b)

Onde a é o primeiro termo e b é o segundo.

 Ao desenvolvermos esse produto, utilizando a propriedade distributiva da multiplicação, teremos:

O quadrado da diferença de dois termos é igual ao quadrado do primeiro termo, menos duas vezes o produto do primeiro termo pelo segundo, mais o quadrado do segundo termo.
Exemplos:

3. O produto da soma pela diferença de dois termos

Se tivermos o produto da soma pela diferença de dois termos, poderemos transformá-lo numa diferença de quadrados.

O produto da soma pela diferença de dois termos é igual ao quadrado do primeiro termo, menos o quadrado do segundo termo.

Exemplos

• (4c + 3d).(4c – 3d) = (4c)² – (3d)² = 16c² – 9d²
• (x/2 + y).(x/2 – y) = (x/2)² – y² = x²/4 – y²
• (m + n).(m – n) = m² – n²

4. O cubo da soma de dois termos

Consideremos o caso a seguir:

(a + b)³ = (a + b).(a + b)² → potência de mesma base.

(a + b).(a² + 2ab + b²) → (a + b)²

Aplicando a propriedade distributiva como nos casos anteriores, teremos:

(a + b)³ = a³ + 3a²b + 3ab² + b³

O cubo da soma de dois termos é igual ao cubo do primeiro termo, mais três vezes o produto do quadrado do primeiro termo pelo segundo, mais três vezes o produto do primeiro termo pelo quadrado do segundo, mais o cubo do segundo termo.

Exemplos:

• (2x + 2y)³ = (2x)³ + 3.(2x)².(2y) + 3.(2x).(2y)² + (2y)³ = 8x³ + 24x²y + 24xy² + 8y³
• (w + 3z)³ = w³ + 3.(w²).(3z) + 3.w.(3z)² + (3z)³ = w³ + 9w²z + 27wz² + 27z³
• (m + n)³ = m³ + 3m²n + 3mn² + n³

5. O cubo da diferença de dois termos

Acompanhem o caso seguinte:

(a – b)³ = (a - b).(a – b)² → potência de mesma base.

 (a – b).(a² – 2ab + b²) → (a - b)²

Aplicando a propriedade distributiva como nos casos anteriores, teremos:

(a – b)³ = a³ – 3a²b + 3ab² – b³

O cubo da diferença de dois termos é igual ao cubo do primeiro termo, menos três vezes o produto do quadrado do primeiro termo pelo segundo, mais três vezes o produto do primeiro termo pelo quadrado do segundo, menos o cubo do segundo termo.

Exemplos

• (2 – y)³ = 2³ – 3.(2²).y + 3.2.y² – y³ = 8 – 12y + 6y² – y³ ou y³– 6y²  +  12y – 8
• (2w – z)³ = (2w)³ – 3.(2w)².z + 3.(2w).z² – z³ = 8w³ – 12w²z + 6wz² – z³
• (c – d)³ = c³ – 3c²d + 3cd² – d³  

Atenciosamente, Professor Leonardo Bezerra.

Poliedros e não-poliedros

1. Definição de poliedro

Poliedro é um sólido geométrico que tem todas as superfícies planas (prismas, pirâmides e outros).

2. Elementos de um poliedro

Um poliedro tem vértices, arestas e faces (bases e faces laterais).

Num prisma:

• existem 2 bases
• o nº de faces laterais é igual ao nº de lados da base
• o nº de arestas é o triplo do nº de lados da base
• o nº de vértices é igual ao dobro do nº de lados da base

Numa pirâmide:

• existe apenas 1 base
• o nº de faces laterais é igual ao nº de lados da base
• o nº de arestas é o dobro do nº de lados da base
• o nº de vértices é mais 1 que o nº de lados da base

3. Classificação de prismas e pirâmides

Os prismas e as pirâmides classificam-se pelo polígono da base.

4. Poliedros regulares

Poliedros regulares são sólidos cujas faces são polígonos regulares e geometricamente iguais.

Platão (sábio grego que viveu por volta dos 400 anos a.C) foi quem estudou os polígonos regulares e por isso são designados sólidos de Platão e estavam relacionados na Grécia Antiga às forças da Natureza.

• Tetraedro (4 faces) – o Fogo
• Cubo (6 faces) – a Terra
• Octaedro (8 faces) – o Ar
• Dodecaedro (12 faces) – a Água
• Icosaedro (20 faces) – o Universo

5. Definição de não-poliedros

Não-poliedros são sólidos geométricos que têm pelo menos uma superfície curva (cone, cilindro, esfera e outros).

6. Elementos de não-poliedros

Um não-poliedro pode ser constituído apenas por uma superfície curva (esfera) ou pode apresentar também superfícies planas. Depende do não-poliedro poderá ter bases e vértices.

Definição

A seguinte definição nos dá uma idéia do que é poliedro, então definiremos assim:

“Poliedro é uma reunião de um número finito de polígonos planos, onde cada lado de um desses polígonos é também lado de um, e apenas um, outro polígono”.

Vejam os seguintes exemplos:

OBS: Podemos também encontrar como definição para poliedros, o seguinte: É um sólido limitado por polígonos, que tem, dois a dois, um lado comum.
Cada poliedro é formado pela reunião de um número finito de regiões poligonais planas, chamadas de faces. Cada lado de uma região poligonal, comum a exatamente duas faces, é chamada aresta do poliedro. E cada vértice de uma face é um vértice do poliedro. Veja:

Fig. 01

Poliedro convexo e Poliedro não-convexo

Observe as figuras abaixo:

Qual dessas figuras você classificaria como poliedro convexo e como poliedro não convexo?
A resposta para essa indagação fica mais fácil quando temos conhecimento de que:

“Um poliedro é convexo se qualquer reta (não paralela a nenhuma de suas faces) o corta em, no máximo, dois pontos”.

Logo, podemos concluir, que o poliedro convexo está representado pela figura 02, e a figura 03 é um exemplo de poliedro não-convexo.

Teorema de Euler

O matemático suíço Leonhard Euler (1707 – 1783) descobriu uma importante relação entre o número de vértice (V), o número de aresta (A) e o número de faces (F) de um poliedro convexo.
O teorema de Euler foi descoberto em 1758. Desde então diversas demonstrações apareceram na literatura e algumas continham falhas (como a de Cauchy), que foram descobertas muitos anos mais tarde. Essas falhas eram devidas à falta de precisão na definição de poliedro. Mesmo Euler nunca se preocupou em definir precisamente essa palavra.
Em todo poliedro com A arestas, V vértices e F faces, vale a relação:

V - A + F = 2

Exercícios Resolvidos

1º) Arquimedes descobriu um poliedro convexo formado por 12 faces pentagonais e 20 faces hexagonais, todas regulares. Esse poliedro inspirou a fabricação da bola de futebol que apareceu pela primeira vez na Copa do Mundo de 1970. Quantos vértices possui esse poliedro?

Resolução:
Como o poliedro tem 12 faces pentagonais, então:
12 . 5  = 60
O poliedro tem 20 faces hexagonais, assim 20 . 6  = 120, logo:  F = 12 + 20 = 32
Cada aresta foi contada duas vezes, portanto temos:
2A = 60 + 120
A = 90
Como o poliedro é convexo, vale a relação de Euler,
V – A + F = 2, portanto:
V – 90 + 32 =2
V = 2 + 90 – 32
V = 60
Assim, o número de vértices é 60.
2º) Determinar o número de arestas e o número de vértices de um poliedro convexo com 6 faces quadrangulares e 4 faces triangulares.
Resolução:
Como o poliedro tem 6 faces quadrangulares, calculamos: 6 . 4 = 24
O poliedro tem 4 faces triangulares: 4 . 3 = 12
Como cada aresta foi contada duas vezes, o número total de arestas é:  A = (24+12)/2 = 18
Temos então F  = 10, A = 18.
Aplicando a relação de Euler:
V – A + F = 2
V – 18 + 10 = 2
V = 10
Logo, o poliedro tem 18 arestas e 10 vértices.

Exercícios para praticar

1º) Determine o número de vértices de um poliedro convexo que tem três faces triangulares, uma face quadrangular, uma face pentagonal e duas faces hexagonais.
2º) (PUC –SP) O número de vértices de um poliedro convexo que possui 12 faces triangulares é:
a) 4                  b) 12                c) 10                d) 6                  e) 8

Atenciosamente, Professor Leonardo Bezerra.

Critérios de divisibilidade

Para alguns números como o dois, o três, o cinco e outros, existem regras que permitem verificar a divisibilidade sem se efetuar a divisão. Essas regras são chamadas de critérios de divisibilidade.

• Divisibilidade por 2

Um número natural é divisível por 2 quando ele termina em 0, ou 2, ou 4, ou 6, ou 8, ou seja, quando ele é par.
Exemplos:
1) 5040 é divisível por 2, pois termina em 0.
2) 237 não é divisível por 2, pois não é um número par.

• Divisibilidade por 3

Um número é divisível por 3 quando a soma dos valores absolutos dos seus algarismos for divisível por 3.
Exemplo:
234 é divisível por 3, pois a soma de seus algarismos é igual a 2+3+4=9, e como 9 é divisível por 3, então 234 é divisível por 3.

• Divisibilidade por 4

Um número é divisível por 4 quando termina em 00 ou quando o número formado pelos dois últimos algarismos da direita for divisível por 4.
Exemplo:
1800 é divisível por 4, pois termina em 00.
4116 é divisível por 4, pois 16 é divisível por 4.
1324 é divisível por 4, pois 24 é divisível por 4.
3850 não é divisível por 4, pois não termina em 00 e 50 não é divisível por 4.

• Divisibilidade por 5

Um número natural é divisível por 5 quando ele termina em 0 ou 5.
Exemplos:
1) 55 é divisível por 5, pois termina em 5.
2) 90 é divisível por 5, pois termina em 0.
3) 87 não é divisível por 5, pois não termina em 0 nem em 5.

• Divisibilidade por 6

Um número é divisível por 6 quando é divisível por 2 e por 3.
Exemplos:
1) 312 é divisível por 6, porque é divisível por 2 (par) e por 3 (soma: 6).
2) 5214 é divisível por 6, porque é divisível por 2 (par) e por 3 (soma: 12).
3) 716 não é divisível por 6, (é divisível por 2, mas não é divisível por 3).
4) 3405 não é divisível por 6 (é divisível por 3, mas não é divisível por 2).

• Divisibilidade por 8

Um número é divisível por 8 quando termina em 000, ou quando o número formado pelos três últimos algarismos da direita for divisível por 8.
Exemplos:
1) 7000 é divisível por 8, pois termina em 000.
2) 56104 é divisível por 8, pois 104 é divisível por 8.
3) 61112 é divisível por 8, pois 112 é divisível por 8.
4) 78164 não é divisível por 8, pois 164 não é divisível por 8.

• Divisibilidade por 9

Um número é divisível por 9 quando a soma dos valores absolutos dos seus algarismos for divisível por 9.
Exemplo:
2871 é divisível por 9, pois a soma de seus algarismos é igual a 2+8+7+1=18, e como 18 é divisível por 9, então 2871 é divisível por 9.

• Divisibilidade por 10

Um número natural é divisível por 10 quando ele termina em 0.
Exemplos:
1) 4150 é divisível por 10, pois termina em 0.
2) 2106 não é divisível por 10, pois não termina em 0.

• Divisibilidade por 11

Um número é divisível por 11 quando a diferença entre as somas dos valores absolutos dos algarismos de ordem ímpar e a dos de ordem par é divisível por 11.
O algarismo das unidades é de 1ª ordem, o das dezenas de 2ª ordem, o das centenas de 3ª ordem, e assim sucessivamente.
Exemplos:
1) 87549
    Si (soma das ordens ímpares) = 9+5+8 = 22
    Sp (soma das ordens pares) = 4+7 = 11
    Si-Sp = 22-11 = 11
    Como 11 é divisível por 11, então o número 87549 é divisível por 11.
2) 439087
    Si (soma das ordens ímpares) = 7+0+3 = 10
    Sp (soma das ordens pares) = 8+9+4 = 21
    Si-Sp = 10-21
    Como a subtração não pode ser realizada, acrescenta-se o menor múltiplo de 11 (diferente de zero) ao minuendo, para que a subtração possa ser realizada: 10+11 = 21. Então temos a subtração 21-21 = 0.
    Como zero é divisível por 11, o número 439087 é divisível por 11.

• Divisibilidade por 12

Um número é divisível por 12 quando é divisível por 3 e por 4.
Exemplos:
1) 720 é divisível por 12, porque é divisível por 3 (soma=9) e por 4 (dois últimos algarismos, 20).
2) 870 não é divisível por 12 (é divisível por 3, mas não é divisível por 4).
3) 340 não é divisível por 12 (é divisível por 4, mas não é divisível por 3).

• Divisibilidade por 15

Um número é divisível por 15 quando é divisível por 3 e por 5.
Exemplos:
1) 105 é divisível por 15, porque é divisível por 3 (soma=6) e por 5 (termina em 5).
2) 324 não é divisível por 15 (é divisível por 3, mas não é divisível por 5).
3) 530 não é divisível por 15 (é divisível por 5, mas não é divisível por 3).

• Divisibilidade por 25

Um número é divisível por 25 quando os dois algarismos finais forem 00, 25, 50 ou 75.
Exemplos:
200, 525, 850 e 975 são divisíveis por 25.

Atenciosamente, Professor Leonardo Bezerra.

Expressão algébrica

Expressões algébricas são expressões matemáticas que apresentam letras e podem conter números, são também denominadas expressões literais. As letras constituem a parte variável das expressões, pois elas podem assumir qualquer valor numérico. No passado as letras foram pouco utilizadas na representação de números desconhecidos, atualmente as letras associadas a números constituem a base da álgebra e contribui de forma eficiente na resolução de várias situações matemáticas. Veja alguns exemplos de expressões algébricas:

2x – 5
3a + 2y
x² + 7x
5 + x – (5x – 2)
10y – 10x
a² – 2ab + b²

As expressões algébricas podem ser utilizadas para representar situações problemas, como as propostas a seguir:

1 – Determine a expressão que representa o perímetro das seguintes figuras:
Perímetro: soma dos lados de qualquer polígono.



4x + 1 + 2x + 4x + 1 + 2x
12x + 2

2x + 6 + 3x – 2 + x + 8
6x + 12


2 – O dobro de um número adicionado a 20: 2x + 20

3 – A diferença entre x e y: x – y

4 – O triplo de um número qualquer subtraído do quádruplo do número: 3x – 4x
 

Valor numérico de uma expressão algébrica

O valor numérico de uma expressão algébrica é o número que pode substituir as incógnitas para que seja efetuada a operação e obtido um resultado final. Observe:
a)  Calcule o valor numérico da expressão algébrica 4x + 10y², para x = 2 e para y = 3.
Resolução:
4 . 2 + 10 . 3² =
8 + 10 . 9 =
8 + 90 = 98
Logo, o valor numérico desta expressão é 98.
Observe que aplicamos corretamente as propriedades das expressões algébricas, começando o cálculo pela potenciação, em seguida a multiplicação e, finalmente, efetuamos a adição.
b) Calcule o valor numérico da expressão algébrica 8x³y², para x = 3 e para y = -1
Resolução:
8 . 3³ . (-1)²
8 . 27 . 1 = 216
Perceba que, nesta expressão, o valor de y é um número negativo, por isso, deve ser escrito entre parênteses.
c)  Encontre o valor numérico da expressão algébrica  + 3y, para x = 9, para y = -2.
Resolução:
 + 3(-2)
3 – 6 = -3
De acordo com a quantidade de termos, as expressões algébricas podem ser classificadas em:

• Monômio – expressão composta por apenas um termo.
  2x⁵
• Binômio – expressão compostas por dois termos.
  y – 6x
• Trinômio – expressão composta por três termos.
  3y² + x – 10
• Polinômio – expressão composta por quatro ou mais termos.
  4ab² + 2a + 3b⁴ + 9

Cada termo de uma expressão algébrica é considerado um monômio. Frequentemente, podem haver repetições de monômios semelhantes na expressão, ou seja, monômios que apresentam base (letra) e expoente iguais. Sempre que isto ocorrer, devemos juntar os monômios semelhantes e escrevê-los em ordem decrescente de acordo com o grau do expoente, de modo a simplificar a equação. Veja um exemplo:
9x² – 4x³ + x – 3 + 6x + 2x² – 10x³ – 7
– 4x³ – 10x³ + 9x² + 2x² + x + 6x – 3 – 7
– 14x³ + 11x² + 7x – 10

Atenciosamente, Professor Leonardo Bezerra.

Equação do 1º Grau com uma Incógnita

Utilizamos uma equação para calcular o valor de um termo desconhecido que será representado por uma letra, cuja representação mais usual se dá por x, y e z. As equações possuem sinais operatórios como, adição, subtração, multiplicação, divisão, radiciação e igualdade. O sinal de igualdade divide a equação em dois membros, os quais são compostos de elementos constituídos por dois tipos:

Elemento de valor constante: representado por valores numéricos.
Elemento de valor variável: representado pela união de números e letras.

Observe exemplos de equações do 1º grau com uma incógnita:

x + 1 = 6
2x + 7 = 18
4x + 1 = 3x – 9
10x + 60 = 12x + 52

Para resolver uma equação, precisamos conhecer algumas técnicas matemáticas. Vamos, por meio de resoluções comentadas, demonstrar essas técnicas.

Exemplo 1:

4x + 2 = 8 – 2x

Em uma equação, devemos separar os elementos variáveis dos elementos constantes. Para isso, vamos colocar os elementos semelhantes em lados diferentes do sinal de igualdade, invertendo o sinal dos termos que mudarem de lado. Veja:

4x + 2x = 8 – 2

Agora aplicamos as operações indicadas entre os termos semelhantes.

6x = 6

O coeficiente numérico da letra x do 1º membro deve passar para o outro lado, dividindo o elemento pertencente ao 2º membro da equação. Observe:

x = 6 / 6
x = 1

Portanto, o valor de x que satisfaz à equação é igual a 1. A verificação pode ser feita substituindo o valor de x na equação, observe:

4x + 2 = 8 – 2x
4 * 1 + 2 = 8 – 2 * 1
4 + 2 = 8 – 2
6 = 6 → sentença verdadeira
Todas as equações, de uma forma geral, podem ser resolvidas dessa maneira.


Exemplo 2:

10x – 9 = 21 + 2x + 3x
10x – 2x – 3x = 21 + 9
10x – 5x = 30
5x = 30
x = 30/5
x = 6

Verificando:

10x – 9 = 21 + 2x + 3x
10 * 6 – 9 = 21 + 2 * 6 + 3 * 6
60 – 9 = 21 + 12 + 18
51 = 51 → sentença verdadeira

O valor numérico de x que satisfaz à equação é 6.


Exemplo 3:

3x – 2x + 10 = 10 + 5x – 40
3x – 2x – 5x = 10 – 40 – 10
3x – 7x = –40
– 4x = – 40

Nos casos em que a parte da variável se encontra negativa, precisamos multiplicar os membros por –1.


– 4x = – 40 * (–1)
4x = 40
x = 40/4
x = 10


Verificando:
3x – 2x + 10 = 10 + 5x – 40
3 * 10 – 2 * 10 + 10 = 10 + 5 * 10 – 40
30 – 20 + 10 = 10 + 50 – 40
20 = 20 → sentença verdadeira


Exemplo 4:

10 – (8x – 2) = 5x + 2(– 4x + 1) → aplicar a propriedade distributiva da multiplicação
10 – 8x + 2 = 5x – 8x + 2
– 8x – 5x + 8x = + 2 – 10 – 2
– 13x + 8x = – 10
– 5x = – 10 * (–1)
5x = 10
x = 10/5
x = 2

Verificando:

10 – (8x – 2) = 5x + 2(– 4x + 1)
10 – (8 * 2 – 2) = 5 * 2 + 2(– 4 * 2 + 1)
10 – (16 – 2) = 10 + 2(–8 + 1)
10 – (14) = 10 + 2(–7)
10 – 14 = 10 – 14
– 4 = – 4 → sentença verdadeira

Equações de primeiro grau

(com uma variável)

    Introdução

    Equação é toda sentença matemática aberta que exprime uma relação de igualdade. A palavra equação tem o prefixo equa, que em latim quer dizer "igual". Exemplos:
2x + 8 = 0
5x - 4 = 6x + 8
3a - b - c = 0

Não são equações:
4 + 8 = 7 + 5   (Não é uma sentença aberta)
x - 5 < 3   (Não é igualdade)
   (não é sentença aberta, nem igualdade)

A equação geral do primeiro grau:

ax+b = 0

onde a e b são números conhecidos e a diferente de 0, se resolve de maneira simples: subtraindo b dos dois lados, obtemos:

ax = -b

dividindo agora por a (dos dois lados), temos:

  
  
   Considera a equação 2x - 8 = 3x -10

   A letra é a incógnita da equação. A palavra incógnita significa " desconhecida".
   Na equação acima a incógnita é x; tudo que antecede o sinal da igualdade denomina-se 1º membro, e o que sucede, 2º membro.

               

   Qualquer parcela, do 1º ou do 2º membro, é um termo da equação.

Equação do 1º grau na incógnita x é toda equação que pode ser escrita na forma ax=b, sendo a e b números racionais, com a diferente de zero.

Atenciosamente, Professor Leonardo Bezerra.

Equação do 2º Grau

Uma equação do segundo grau possui uma incógnita de expoente 2. O método de Bhaskara é uma opção para encontrar os resultados desse tipo de equação.

Uma equação é uma expressão matemática que possui em sua composição incógnitas, coeficientes, expoentes e um sinal de igualdade. As equações são caracterizadas de acordo com o maior expoente de uma das incógnitas. 

Veja:

• 2x + 1 = 0. O expoente da incógnita x é igual a 1. Dessa forma, essa equação é classificada como do 1º grau.
• 2x² + 2x + 6 = 0. Há duas incógnitas x nessa equação, e uma delas possui expoente 2. Essa equação é classificada como do 2º grau.
• x³ – x² + 2x – 4 = 0. Nesse caso, temos três incógnitas x, e o maior expoente – no caso, expoente 3 – torna a equação como do 3º grau.

O que são raízes ou soluções de uma equação do 2º grau?

Cada modelo de equação possui uma forma de resolução. Trabalharemos a forma de resolução de uma equação do 2º grau por meio do método de Bhaskara . Determinar a solução de uma equação é o mesmo que descobrir suas raízes, isto é, o valor ou os valores que satisfazem a equação. As raízes da equação do 2º grau x² – 10x + 24 = 0, por exemplo, são x = 4 ou x = 6, pois:

Substituindo x = 4 na equação, temos:

x² – 10x + 24 = 0
4² – 10 * 4 + 24 = 0
16 – 40 + 24 = 0
–24 + 24 = 0
0 = 0 (verdadeiro)

Substituindo x = 6 na equação, temos:

x² – 10x + 24 = 0
6² – 10 * 6 + 24 = 0
36 – 60 + 24 = 0
– 24 + 24 = 0
0 = 0 (verdadeiro)

Podemos verificar que os dois valores satisfazem a equação, mas como podemos determinar os valores que tornam a equação uma sentença verdadeira? É essa forma de determinar os valores desconhecidos que abordaremos a seguir.

Método de Bhaskara

Vamos determinar pelo método resolutivo de Bhaskara os valores da seguinte equação do 2º grau: x² – 2x – 3 = 0.

Uma equação do 2º grau possui a seguinte lei de formação: ax² + bx + c = 0, em que a, b e c são os coeficientes. Portanto, os coeficientes da equação x² – 2x – 3 = 0 são a = 1, b = –2 e c = –3.

Na fórmula de Bhaskara, utilizaremos somente os coeficientes. Veja:

1º passo: determinar o valor do discriminante ou delta (∆)

∆ = b² – 4.a .c
∆ = (–2)² – 4.1.(–3)
∆ = 4 + 12
∆ = 16

2º passo:

x = – b ± √∆
      2∙a

x = –(– 2) ± √16
       2∙1

x = 2 ± 4
     2

x' = 2 + 4 = 6 = 3
   2       2

x'' = 2 – 4 = – 2 = – 1
2        2

Os resultados são x’ = 3 e x” = –1.

Exemplo II: Determinar a solução da seguinte equação do 2º grau: x² + 8x + 16 = 0.

Os coeficientes são:

a = 1
b = 8
c = 16

∆ = b² – 4 * a * c
∆ = 8² – 4 * 1 * 16
∆ = 64 – 64
∆ = 0

x = – b ± √∆
     2∙a

x = – 8 ± √0
     2∙1

x' = x'' = –8 = – 4
    2

No exemplo 2, devemos observar que o valor do discriminante é igual a zero. Nesses casos, a equação possuirá somente uma solução ou raiz única.

Exemplo III: Calcule o conjunto solução da equação 10x² + 6x + 10 = 0, considerada de 2º grau.

∆ = b² – 4.a .c
∆ = 6² – 4 .10.10
∆ = 36 – 400
∆ = –364

Nas resoluções em que o valor do discriminante é menor que zero, isto é, o número é negativo, a equação não possui raízes reais.

Atenciosamente, Professor Leonardo Bezerra.

Potências

Introdução à história

 A ideia de potência é muito antiga e desde tempos remotos suas aplicações facilitaram a vida humana auxiliando, tornando possíveis muitas representações matemáticas e solucionando problemas de elevado grau de complexidade. Assim como todas as descobertas do homem, a equação possibilitou novos horizontes e permitiu a expansão dos conhecimentos humanos norteando viagens inimagináveis pelos campos abstratos da matemática e alicerçando ciências afins como a astronomia, física, química e biologia.

Conceitos antigos dos quais se têm registros datam do século III a.C. através do astrônomo e inventor Arquimedes em sua tentativa de calcular quantos grãos de areia seriam necessários para encher o universo. Nessa época, tinha-se a ideia de que as estrelas limitavam o nosso universo dando-lhe um formato esférico e, ao calcular o volume dessa esfera astronômica, chegaria ao resultado desejado. Após longo estudo e dedicação, Arquimedes conseguiu encontrar um resultado assombrosamente grande em termos de representação numérica e soube que seria impossível demonstrar sua resposta para que outros conseguissem compreendê-la.

Após séria análise detalhada dos números que apareciam no cálculo do volume da esfera gigante, Arquimedes percebeu um fato curioso: havia uma grande repetição de multiplicações que envolviam o número 10. Surgiu então a ideia de representar sua resposta usando potência de base 10. Hoje utilizada como notação científica e aplicada a várias áreas do conhecimento humano, através da potência de base dez, podemos escrever a resposta conquistada por Arquimedes como 10⁶³.

Toda notação moderna que se tem de potência teve fundamento com o Matemático francês René Descartes (1596-1650) no século XVII. Descartes, além de suas contribuições referentes à potenciação é também conhecido como Pai da Filosofia e da Matemática Modernas.

Onde estão as potências?

A resposta à pergunta anterior seria em nosso cotidiano.  Acompanhem alguns exemplos a seguir:

• Um jogo de xadrez é formado por um tabuleiro tipo 8 x 8 e representa uma matriz quadrada de ordem 8. Podemos calcular o número de casas desse tabuleiro utilizando conhecimentos sobre potência. Para isso, elevamos o número de linhas (8) ao número de colunas (8), ficando 8² = 64.
• Num sítio, as laranjas extraídas periodicamente, são embaladas em forma cúbica: 4 laranjas no comprimento, 4 na largura e 4 na altura. Se desejarmos saber quantas dessas frutas têm nesses cubos, elevamos ao 4, o número de vezes que ele se repete (3), ficando 4³ = 64.

Lembro aos caros leitores que o objetivo do artigo não é apenas mostrar as aplicações das potências em nosso cotidiano, e sim, mostrar-lhes os seus conceitos, propriedades e resoluções, a fim de que abstraiam esses conhecimentos e utilizem-no para tornar suas vidas mais práticas. Quando conseguimos compreender bem um conteúdo, saberemos onde melhor se encaixará a sua aplicação.

Definição e resolução

Potência é todo número na forma aⁿ, com a ≠ 0.

a é a base, n é o expoente e aⁿ é a potência.

aⁿ = a x a x a x a x...a (n vezes)

Por convenção, admitiremos que todo número elevado a 0 é igual a 1, a⁰ = 1 e todo número elevado a 1 é igual a ele próprio, a¹ = a.

Exemplos

2¹ = 2                          54⁰ = 1                              4⁴ = 256                             5³ = 125

Potência de base racional

Para resolver uma potência cuja base é um número fracionário, elevamos tanto o numerador quanto o denominador da fração ao expoente dado.

Exemplo

Potência de expoente negativo

A ideia de inverso é utilizada para solucionar potências de expoente negativo, transformamos numerador em denominador, e vice-versa, logo após, tornamos o expoente positivo.

Exemplos

Multiplicação de potências de mesma base

Resolvemos a multiplicação de potências de mesma base conservando uma das bases e adicionando os expoentes.

a­^m . aⁿ  =  a^{m + n}

Exemplos

Divisão de potências de mesma base

Toda divisão de potências de mesma base, com esta diferente de zero, pode ser resolvida conservando uma das bases e subtraindo os expoentes.

a^m : aⁿ = a^{m – n}, com a ≠ 0.

Exemplos

Multiplicação de fatores elevados ao mesmo expoente

Para o produto de dois ou mais fatores elevados ao mesmo expoente, elevamos cada um dos fatores ao expoente dado na questão.

(a . b)ⁿ = aⁿ . bⁿ

Exemplos

(5 . 6)⁴ → 5⁴ . 6⁴                                         (0,2 . 1,3)³ → (0,2)³ . (1,3)³

Divisão de expoente igual

Aqui segue-se o mesmo critério dado na propriedade anterior: eleva-se o dividendo e o divisor ao mesmo expoente.

(a : b)ⁿ = aⁿ : bⁿ

Exemplos

(9 : 8)⁵ = 9⁵ : 8⁵                                                 (2,3 : 0,1)² = (2,3)² : (0,1)²

Potência de potência

Quando elevamos uma determinada potência à outra potência, temos uma potência de potência. Para resolvê-la, podemos conservar a base e multiplicar os expoentes.

(a^m)ⁿ = a^{m . n}

Exemplos

(2³)⁴ → 2^{3 . 4} = 2¹²                                             [(1/5)²]⁵ → (1/5)^{2 . 5} = (1/5)¹⁰

Potência de base 10

A potência de base 10 é utilizada para abreviar a escrita de números que contenham n fatores 10, facilitando assim sua representação.

Exemplos

10⁵ = 100000 (5 zeros)

10⁷ = 10000000 (7 zeros)

10³ = 1000 (3 zeros)

Nesse tipo de potência, quanto o expoente for positivo, ele indica a quantidade de zeros que deverão ser acrescentados após o algarismo 1.

10^-2 = 0,01 (2 casas decimais)

10^-5 = 0,00001 (5 casas decimais)

Aqui, como o expoente é negativo, ele indica o número de casas decimais que deverão ser criadas a partir do zero e com final 1.

Um bom exercício de revisão para a prova: http://www.coladaweb.com/exercicios-resolvidos/exercicios-resolvidos-de-matematica/potenciacao

Obrigado pela leitura, um grande abraço e até a próxima! 

Professor Leonardo Bezerra

Origem do sistema de numeração decimal, egípcio e romano

1. Introdução

O zero sempre existiu?

2. Origem do sistema de numeração decimal

Contar [do latim computare]: calcular, fazer contas, estimar, avaliar, numerar, recensear, marcar, registrar. Contagem: ação de contar, cômputo, apuração, escore.

Já vimos que um sistema de numeração se constitui de regras, utilizando-se de símbolos para representar os números.

O sistema de numeração decimal ou de base 10 que usamos nos dias de hoje não foi criado de um dia para outro.

A necessidade de contar fez com que os homens criassem modos de comparar quantidades; por exemplo: como contar ovelhas de um rebanho e saber se nenhuma se havia desgarrado. Podia-se associar uma pedra com uma ovelha, ou com um pedaço de madeira entalhado ou com um dedo da mão ou um nó de corda. Veja os exemplos ao lado.

Como contar grandes quantidades?

Com o surgimento da escrita, tudo se tornou mais fácil e foram aparecendo diferentes sistemas de representar grandes quantidades. Isso fez com que alguns sistemas de numeração caíssem em desuso, devido à forma de representação e à grande quantidade de repetições de um mesmo símbolo para uma quantidade considerada “pequena", como, por exemplo, a representação de 9999 no sistema de numeração egípcio, que você irá ver mais tarde.

Há mais de 2000 anos, o sistema de numeração utilizado pelos hindus era parecido com o sistema de numeração grego e foi-se modificando com o passar dos tempos.

Com a tradução de uma obra hindu, pelos árabes, no século VIII d.C., seu sistema de numeração passou a ser conhecido pelos estudiosos árabes.

No século IX d.C., um matemático árabe chamado Mohamed ibn Musa al-Khwarizmi (daí a origem da  palavra "algarismo") passou a estudar o sistema de numeração hindu, colocando seus manuscritos em um livro traduzido na Europa e divulgado com a expansão da cultura árabe.

Por essa razão, o sistema de numeração decimal é chamado de sistema hindu-arábico ou indo-arábico.

Até chegarmos aos dez símbolos indo-arábicos – 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 – que hoje utilizamos, houve muitas modificações na sua forma. Veja, por exemplo, a representação dos numerais pelos árabes orientais no século XVI d.C. e que ainda é utilizada:

Observe formas de escrita do numeral 7 por diferentes povos, alguns com uso das letras do alfabeto.

3. Sistema de numeração egípcio

Há cinco mil anos, os egípcios usavam um sistema de numeração em que não existia um símbolo para o zero. Sua escrita hieroglífica era usada em monumentos e em obras literárias escritas em papiro.

Os algarismos hieroglíficos egípcios são:

               

  Exemplos:

Características do sistema de numeração egípcio:

• É aditivo, isto é, os valores dos símbolos são somados uns aos outros para representar as quantidades.
  
  
• Não é posicional, isto é, o valor do número não depende da posição dos símbolos na sua representação.
  
  
  
• Utiliza a base 10. Note que a cada grupo de 10 símbolos iguais corresponde um outro símbolo.
  
  

4. Sistema de numeração romano

Há cerca de 2000 anos, os romanos usavam um sistema de numeração que também não possuía um símbolo para o zero.

Os algarismos romanos são:

I	V	X	L	C	D	M
1	5	10	50	100	500	1000

Exemplos:

Podemos escrever:

MMM = 3000 ou III = 300

Quando um traço horizontal é colocado acima do símbolo, ele fica multiplicado por 1000; dois traços horizontais, por 1 000 000; e assim por diante

Características do sistema de numeração romano:

• Não é exclusivamente aditivo, pois, conforme a colocação, seus símbolos são somados ou subtraídos. Verifique:
• a) Dois ou três símbolos iguais, escritos lado a lado, são somados.

Exemplos:

II = 2                                        III = 3                                           XXX = 30
1 + 1 = 2                                   1 + 1 + 1 = 3                                 10 + 10 + 10 = 30

CC = 200                                   MMM = 3000
100 + 100 = 200                         1000 + 1000 + 1000 = 3000

b) Um símbolo de menor valor, escrito à direita de outro símbolo de maior valor, é somado.

Exemplos:

XII = 12                                    CXXX = 130                                  MDI = 1501
10 + 1 + 1                                 100 + 10 + 10 + 10                        1000 + 500 + 1

c) Um símbolo de menor valor, escrito à esquerda de outro símbolo de valor maior, é subtraído do símbolo de valor maior.

Exemplos:

IX = 9                                       CD = 400                                      CM = 900
10 - 1 = 9                                  500 - 100 = 400                            1000 - 100 = 900

d) É posicional, de certa forma, pois o valor do número depende da posição dos símbolos.

Exemplos:

XII = 12                                     MDC = 1600                                  XL = 40
IX = 9                                        MCD = 1400                                  LX = 60

e) Não possui uma base definida. Os símbolos que podem ser repetidos até 3 vezes são I, X, C e M, enquanto os símbolos V, L e D nunca são repetidos.

Exemplos:

Repetimos no máximo 3 vezes:

III = 3                                        XXX=30
CCC = 300                                  MMM = 3000

Não podemos escrever:

	escrevemos X
	escrevemos XV
	escrevemos C
	escrevemos CL
	escrevemos M
	escrevemos MD

Observação: O número 4 era escrito IIII, como se vê em relógios antigos, principalmente em catedrais. Hoje, 4 = IV.

Nos dias de hoje, o sistema de numeração romano é usado para indicar capítulos em livros, séculos, em relógios etc.

Estamos no século XXI d.C. (século é um período de cem anos), no terceiro milênio (período de mil anos) e na primeira década (período de dez anos).

Considerando séculos e milênios (d.C.), temos:

século I                     - do ano 1 ao ano 100
século II                    - do ano 101 ao 200
                                             
século XV                  - do ano 1401 ao ano 1500
                                            
século XVIII               - do ano 1701 ao ano 1800
século XIX                 - do ano 1801 ao ano 1900
século XX                  - do ano 1901 ao ano 2000
século XXI                 - do ano 2001 ao ano 2100

primeiro milênio           - do ano 1 ao ano 1000
segundo milênio          - do ano 1001 ao ano 2000
terceiro milênio           - do ano 2001 ao ano 3000

O descobrimento do Brasil ocorreu em 22/4/1500, ou seja, no século XV e no segundo milênio.

Em algarismos romanos, temos:

XXII / IV / MD

A Proclamação da República ocorreu em 15/11/1889, ou seja, no século XIX e no segundo milênio.

Em algarismos romanos, temos:

XV / XI / MDCCCLXXXIX

A inauguração de Brasília ocorreu em 21/4/1960, ou seja, no século XX e no segundo milênio.

Em algarismos romanos, temos:

XXI / IV / MCMLX

Quais as vantagens do sistema de numeração decimal?

O sistema de numeração decimal é multiplicativo posicional e apresenta o valor posicional (relativo) do algarismo.

Exemplo:

No número 4567, o valor relativo do 4 é 4000, do 5 é 500, do 6 é 60 e do 7 é 7.

Obrigado pela leitura, um grande abraço e até a próxima! 

Professor Leonardo Bezerra